2019-01-19

行列式の計算

数学

先の記事
amori.hatenablog.com
で省略した、超立体の体積計算でのグラム行列式の計算は、普通に行列式計算の展開をすれば求まります。
以下がその過程です。
＃意外にも最後に二項定理がでてきます。

対角要素が１、その他要素をp として一般化します。

（2022/02/06追記）
さらに一般化したものはこちらです。
行列の非対角成分が一様な場合の行列式 - amori's blog

グラム行列式についてはもっと簡単な計算方法がありました。
$D_n = \left| \begin{array}{ccccc} 1 & p & \cdots & p & p\\ p & 1 & p & p & p\\ \vdots & p & \ddots & p & \vdots\\ p & p & p & 1 & p\\ p & p & \cdots & p & 1 \end{array} \right|$
2行目以降から1行目を引きます。
$D_n = \left| \begin{array}{ccccc} 1 & p & \cdots & p & p\\ p-1 & 1-p & 0 & 0 & 0\\ \vdots & 0 & \ddots & 0 & \vdots\\ p-1 & 0 & 0 & 1-p & 0\\ p-1 & 0 & \cdots & 0 & 1-p \end{array} \right|$
2列目以降を1列目に足して1列目2行目以降をゼロにします。
$D_n = \left| \begin{array}{ccccc} 1-(n-1)p & p & \cdots & p & p\\ 0 & 1-p & 0 & 0 & 0\\ \vdots & 0 & \ddots & 0 & \vdots\\ 0 & 0 & 0 & 1-p & 0\\ 0 & 0 & \cdots & 0 & 1-p \end{array} \right|$
三角行列になったので、
$D_n =(1-(n-1)p)(1-p)^{n-1} \\ =(1-p)^n +np(1-p)^{n-1} \\$

（追記終わり）********************
(以下、旧記載）
対角要素が１、その他要素をp として一般化します。
$D_n = \left| \begin{array}{ccccc} 1 & p & \cdots & p & p\\ p & 1 & p & p & p\\ \vdots & p & \ddots & p & \vdots\\ p & p & p & 1 & p\\ p & p & \cdots & p & 1 \end{array} \right|$
計算しやすいように分離します。
$= \left| \begin{array}{ccccc} 1-p & p & \cdots & p & p\\ 0 & 1 & p & p & p\\ \vdots & p & \ddots & p & \vdots\\ 0 & p & p & 1 & p\\ 0 & p & \cdots & p & 1 \end{array} \right| + \left| \begin{array}{ccccc} p & p & \cdots & p & p\\ p & 1 & p & p & p\\ \vdots & p & \ddots & p & \vdots\\ p & p & p & 1 & p\\ p & p & \cdots & p & 1 \end{array} \right|$

第2項を,1行1列の要素がpである行列として、その行列式をD'とします。
$= (1-p) D_{n-1} + D'_n$
D'を展開します。
$D'_n= \left| \begin{array}{ccccc} p & p & \cdots & p & p\\ p & 1 & p & p & p\\ \vdots & p & \ddots & p & \vdots\\ p & p & p & 1 & p\\ 0 & 0 & \cdots & 0 & 1-p \end{array} \right|$

$= (-1)^{n+n}(1-p) \left| \begin{array}{cccc} p & p & \cdots & p \\ p & 1 & p & p \\ \vdots & p & \ddots & \vdots \\ p & p & \cdots & 1 \end{array} \right| = (1-p) \cdot D'_{n-1}$
よって、 $D'_n=(1-p)^{n-2} D'_2$
$D'_2 = \left| \begin{array}{cc} p & p \\ p & 1 \end{array} \right| = p-p^2=p(1-p)$ 　なので
$D'_n=(1-p)^{n-1} p$

もとの式に戻します。見やすいように $1-p = \alpha$ として、
$D_n = \alpha D_{n-1} +\alpha^{n-1}(1-\alpha)$
これをn=2まで展開し、
$\alpha D_{n-1} = \alpha^2 D_{n-2} +\alpha\cdot\alpha^{n-2}(1-\alpha)$
$\vdots = \vdots$
$\alpha^{n-2}D_2 = \alpha^{n-1} D_1 +\alpha^{n-2}\cdot\alpha(1-\alpha)$
すべて合計すると右辺左辺の $D_k$ が相殺され、
$D_n = \alpha^{n-1} D_1 +(n-1)\alpha^{n-1}(1-\alpha)$

$D_1 = 1$ なので、
$D_n = \alpha^{n-1}(1+(n-1)(1-\alpha)) = \alpha^n + n\alpha^{n-1}(1-\alpha)$
$\alpha = 1-p$ に戻して、

$D_n = (1-p)^{n} + n\cdot (1-p)^{n-1}\cdot p$
これ、2項定理の最初の2項の和ですね。なんでかわかりませんがｗ

というわけで、 $p=\frac{1}{2}$ の時は　 $D_n = \frac{n+1}{2^n}$ となります。

2019-01-18

超立体の体積(容積)計算

数学

不勉強なことにグラム行列というものを知りませんでした。機械学習関係の解説でちょいちょい目にしますが、そちらはわたしには高尚過ぎますので、シンプルにグラム行列式が体積計算に便利(なこともある)ということ改めて知ったというお話です。

例えば、３つのベクトルがなす平行六面体の体積Vは、そのベクトルからなる3×3行列、仮にAとして、その行列式|A|から求められます。
$A = [\bf{a}, \bf{b}, \bf{c} ] = \left[ \begin{array}{ccc} a_{x} & b_{x} & c_{x} \\ a_{y} & b_{y} & c_{y} \\ a_{z} & b_{z} & c_{z} \end{array}\right]$
$V= |A| = a_{x}b_{y}c_{z} +a_{y}b_{z}c_{x} +a_{z}b_{x}c_{y} -a_{z}b_{y}c_{x} -a_{y}b_{x}c_{z} +a_{x}b_{z}c_{y}$

グラム行列は、AとAの転置の積
$A^{\mathrm{T}}A$
$= \left[ \begin{array}{ccc} |\bf{a}|^{2} & \bf{a} \bf{b} & \bf{a} \bf{c} \\ \bf{b} \bf{a} & |\bf{b}|^{2} & \bf{b} \bf{c} \\ \bf{c} \bf{a} & \bf{c} \bf{b} & |\bf{c}|^{2} \end{array}\right]$
なのでグラム行列式は平行六面体の体積の二乗になるのは明らかです。

わざわざ積をとるのが何で便利かというと、グラム行列の要素が全部、元のベクトルの内積となりベクトルの要素を直接計算しなくてよくなるのです。

正四面体のように辺と角の関係がシンプルな場合だと計算が実に単純になります。
各ベクトルは長さ1、ベクトルがなす角は60度なので内積は全て1/2。
$\displaystyle G = \left[ \begin{array}{ccc} 1 & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 1 & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 1 \end{array}\right]$

グラム行列式は、対角要素が全て1、その他が1/2なので、行列式は

$1+\frac{1}{8} +\frac{1}{8} -\frac{1}{4} -\frac{1}{4} -\frac{1}{4}=\frac{1}{2}$
これのルートが平行六面体の体積で、正四面体はその1/6で、 $\frac{\sqrt{2}}{12}$ となります。

この計算は4次元以上についても全く同じで、正四面体の4次元の拡張である5胞体については、4次のグラム行列式を求めればよいわけです。
対角要素が1、他が1/2であるn次行列の行列式は、一般に
$\frac{n+1}{2^n}$
となります。
#詳細は以下の記事を参照ください。
amori.hatenablog.com
さらに一般化した行列式計算はこちらです。
amori.hatenablog.com

よってn次元の超三角錐は、
$\frac{1}{n!}\sqrt{\frac{n+1}{2^n}}$
となります。
5胞体は、n=4で超体積は $\frac{\sqrt{5}}{96}$ です。
https://ja.m.wikipedia.org/wiki/正五胞体
ちなみに、2次元は正三角形の面積、 $\frac{\sqrt{3}}{4}$ になってますね。

2019-01-15

22/7 計算中が面白くなってた

22/7 というとπの近似値なのですけど、グループ名の由来と関係あるのかようわかりませんw

冠番組の「22/7計算中」はアニメに分類されてたのでたまたまチェックしただけで、さっさと切ろうと思いつつ、なんか惰性でかけ流すうちに各キャラが立ってきて視聴が続いていたりします。

いやね、せっかくヴァーチャル化してるのにロケを観ながらのスタジオでひな壇のリアクションだけってゆるすぎるでしょ、と思ってたのですが、まあ、それが逆にキャラの差別化やタチ加減を浸透させる効果があったのかもしれません。

まあ、こんな感じでゆるゆると続くんだろうと思ってところに、歌合戦企画で動く動く(^｡^)(除くパネル組)
キャラに馴染んでる分、はっきり言ってヴァーチャルのど自慢より楽しかったぞ。

今回の企画で、22/7の本来の狙いがようやく形になったのではないかな。

今後もスタジオでガンガン動くネタをやって欲しいぞ。

追記
残念ながら、この企画は相当にモーションキャプチャの負担が(多分エンジニアに)大きかったようで、これ以降はもーしょう4名+パネル2名という省エネ形式が固定してしまった・・・年度予算が尽きたのかも。
けど、番組としては安定して面白くなってきたなあ。何と言っても各自のキャラが安定してきて、メンバーが企画のメリハリにうまい具合に乗っかれるようになってきたと思います。
司会の三四郎の仕切りに頼ることがかなり少なくなってきてるのも明らかかと。

2019-01-14

GXRスナップ: Season'a Greetings

カメラ GXR スナップロンドンクリスマス

みなさま、よいお年をお過ごしください。

2018-12-23

ボケ光学

カメラ GR 数学 GXR

友人とカメラの話をしていて
「焦点距離長いほうがボケさせられる」という話題になり、
そう言えば、定量的にちゃんと理解してないなあ、と思いザクッと検索してみました。
ぱっと見つかる解説では、なんかフワッとした説明ばっかりだったので、あらためて自分なりに理解を整理してみるために、レンズの公式から焦点とボケの関係を導出してみました。

その結果、自分の理解も中途半端だったことがわかりました（＾＾；

◾️えぐぜくてぃぶさまり

数式から正確に解説をすると結構な分量になってしまったので、とりあえず結論だけ先にまとめます。

前提：ボケの大小は最終的な画像の大きさを揃えて比較する。
結論
（1）被写体の近くのボケについてはレンズの焦点距離による違いは（ほぼ）ない。
（2）被写体から十分離れた背景のボケは焦点距離が長いほど、よりボケる
（3）焦点距離が長いほど背景が大きくなり、一般に画面の粒度大きくなるので、（2）の影響と相まって「焦点距離が長いほどよくボケる」という効果がある

一般に「焦点距離が長いほどボケる」というのは（3）の意味で使われていると思われます。
しかし、巷の解説や議論をみると、なんとなくではありますが、
（2）（3）のボケとボケの元対象の相互作用はあんまり意識されておらず、（1）に至っては「被写体近傍でも焦点距離が長いほうがよりボケる」と少なからず勘違いされているのではないかと感じます。

以上が結論です。
では、数式により解釈についてご興味があるかたは次にお進みください。

◾️前提条件

まず前提と比較の条件について。

ボケの大きさに関する要素は、
・焦点距離
・絞り値
・被写体まで距離
・ボケ対象との距離
・センササイズ
があります。
ボケの大小を比較するにあたり、最終的な画像の大きさ・被写体の大きさを揃えた時のボケの大きさの違いを比較するものとします。
簡単に言うと、ポートレート写真を撮るとして、広角・望遠どちらもバストショットとして揃えるので、広角ならばより近くで撮ることで条件を揃える、ということです。

◾️導出

ピントとボケの関係はレンズの公式によって計算できます。

$\displaystyle \frac{1}{a} + \frac{1}{b} = \frac{1}{f}$
f: レンズの焦点距離
a: レンズから光源までの距離（つまり被写体までの距離）
b: レンズから像が結ばれている点までの距離（つまりピントが合っているセンサまでの距離）

（詳しくはWikipedia:レンズの公式を参照のこと）
https://ja.m.wikipedia.org/wiki/

これを踏まえて、ボケとは
「ボケている対象（ボケ光源）の点光源が、センサー上を照らすエリア」
とし、ボケの大きさとはこのエリアの大きさとします。

下記の図は、ピントとボケの関係を示しています。

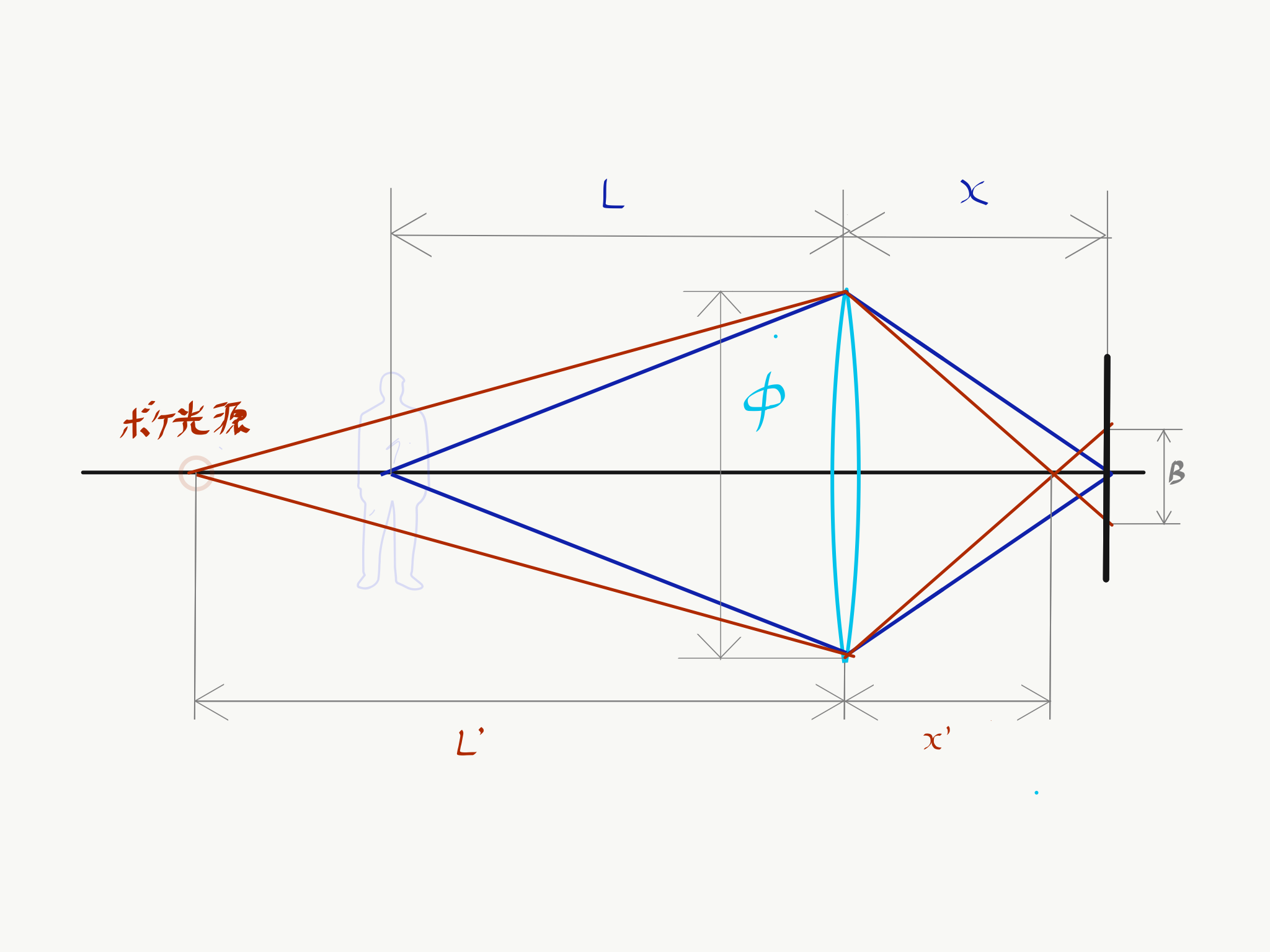
φ: レンズの開口径(mm)
B: ボケの大きさ(mm)
f: レンズの焦点距離(mm)
L:レンズから被写体までの距離(mm)
x:被写体のピントがあっている状態でのレンズからセンサーまでの距離 (mm)
L' : レンズからボケ光源までの距離(mm) ※図は L' > L つまり遠い場合
x': ボケ光源が結像する距離(mm)

φとBがなす三角形の相似関係
$\frac{\phi}{x} = \frac{B}{x - x'}$
なので、被写体とボケ光源それぞれのレンズの公式
$\frac{1}{L} + \frac{1}{x} = \frac{1}{f}$
$\frac{1}{L'} + \frac{1}{x'} = \frac{1}{f}$
を適用すると、
$B = \phi \frac{ \frac{1}{L} - \frac{1}{L'}}{\frac{1}{f}-\frac{1}{L}}$
となります。
焦点距離とボケの関係を明確にするために式を変形します。
あと、φと絞り値 Fの関係 $\displaystyle F=\frac{f}{\phi}$ で、式のパラメタを絞り値に変更すると、

$B = \frac{1}{F}\cdot\frac{f^{2}}{L^{2}} \cdot \frac{d}{1+\frac{d}{L} } \cdot \frac{1}{1-\frac{f}{L}}$
となります。なお、

$d = L' - L$
で、被写体とボケ光源の距離です。

この式の4つのそれぞれの項から、焦点距離とボケの関係を定量的に把握できます。
各項について説明します。

第1項： $\frac{1}{F}$

絞り値Fはこの項にのみ現れます。なので、単純にFが小さければ、つまり絞りをひらくとボケる、ということに相当します。撮影条件として固定できます。

第2項： $\frac{f^{2}}{L^{2}}$

これが結論（1）の「被写体の近くのボケについてはレンズの焦点距離による違いは（ほぼ）ない。」理由です。f（焦点距離）の二乗に比例してボケは大きくなりますが、L（被写体までの距離）の二乗に反比例してボケは小さくなります。前提条件にあったように、被写体の大きさが同じになる距離は焦点距離に比例します。例えば5m先の被写体をf=50mmのレンズと同じ大きさになるようにf=28mmのレンズでとる場合の距離は2.8mです。
よって、この項の分子分母の値の焦点距離の違いは相殺されます。これが焦点距離の違いはボケに影響しないという理由です。
ここで「被写体近くの」としているのは、被写体近くではない場合は第3項の影響が優位になるからです。また「ほぼ違いがない」としているのは第4項が無視できることを想定しているからです。
詳細はそれぞれの項の説明を参照ください。

第3項： $\frac{d}{1+\frac{d}{L} }$

分母のd/Lは、ボケ光源と被写体と近く、d/Lが十分に小さい場合、分母はほぼ1となり、その結果、分子のdのみが有意となり、この項の意味は「ボケ光源が遠いほどボケが大きい」を意味することになり、f、Lの影響が無視できることになります。
d＞＞L、つまりボケ光源が背景に相当するほど離れている場合についてはLが有意になりますが、これについては別途説明します。

第4項： $\frac{1}{1-\frac{f}{L}}$

f/Lが十分小さい場合、つまり、焦点距離に対して被写体の処理が十分遠いばあい、要るするに接写以外はこの項はほぼ1となり影響は無視できます。
逆にこの項が無視できない条件、例えばf=50mm, L= 100mmという接写の場合、この項の値は2となり、他の項のボケの影響がさらに2倍になるということに相当します。

以下、整理します。

◾️焦点距離がボケに影響しない場合

被写体が接写とならない程度に離れている場合、被写体のそばのボケは焦点距離に影響しません。
例えばポートレートを撮っている時に、眼にピントを合わせてそれ以外の髪や服へのピントをコントロールする場合は基本的に絞り調整しか効かないので、ズームを使う場合は接写／マクロの領域でのコントロールが必要ということになります。

◾️被写体から十分離れた背景のボケは焦点距離が長いほど、よりボケる

これは第3項で、d≒L からd＞Lの場合は、d/Lが有意となるからで、第3項を変形すると、
$\frac{L}{L/d+1}$
なので、dが大きくなるほど、この項はLに近づきます。これにより第2項の分母がLの2乗からLとなり、第2項はfとLのみが相殺され、最終的にfに比例してボケが大きくなるということになります。
つまり焦点距離に比例してボケが大きくなるということになります。

◾️焦点距離が長いほど背景が大きくなり、ボケの効果が強くなる

上記までの検討は、ボケを点光源として計算していましたが、被写体よりも十分に遠い（距離にして数倍程度以上）ボケの対象を面として検討する場合、いわゆるボケの全体は、

ボケ対象＋ボケによる滲み

ボケの対象の大きさは、焦点距離が大きくなるといわゆる「圧縮効果」で相対的に大きくなります。またボケによる滲みは第3項によってさらに大きくなり、これによりボケ全体が大きくなります。

◾️まとめ

以上を再度まとめますと、

焦点距離が長い場合、背景のボケがより大きくなる。特にボケの滲み部分が焦点距離に比例する。

被写体までの距離が焦点距離に近くなるに従い、よりボケが大きくなる

となります。

◾️おまけ：センサーサイズの違いの影響

なお、フルサイズとAPSーC・マイクロフォーサイズというセンサーサイズの違いによるボケの変化は、35mm換算の焦点距離が同じという条件での撮影を考えると、同様の考察が可能です
・画角が同じ、つまり、被写体までの距離は同じ
・焦点距離がセンサーサイズに比例して短くなる
・ボケの大きさのサイズ分変換は、センサーサイズに比例する

以上から、センサーサイズに比例してボケる、というなり、背景のボケの影響は上記の考察がそのまま適用されるので、結論として

センサーサイズが大きいと、よりボケる

という結論になります。
これは定説通りですね。

2018-12-22

GXRスナップ: 駆ける

GR カメラ GXR 水戸スナップ

川沿いに散歩してる時に見える景色が、絵になるなあ、と思うことが多いです。

これはたぶん、向こう岸の土手が左右に長く見渡せることで、安定した構図の景色が見られるからなのでしょう。

amori's blog

よろず技術系と趣味関係の雑記です。アニメの比重が高くなってます・・